sanoreo.blogg.se - Quadratic inequalities

QUADRATIC INEQUALITIES HOW TO

We also know the endpoints are excluded since 3 creates a denominator of zero and we have a strict inequality. $$(-2)^2 - 5(-2) - 6 > 0$$ $$4 + 10 - 6 > 0$$ $$\require$$ Since the test of the number 4 produces a false statement, we know values that are greater than 4 will not satisfy the inequality.

Let's choose -2, we will plug this in for x in the original inequality. Let's begin with interval A, we can choose any value that is less than -1. \displaystyle ax2+bx+c > 0 ax2 +bx+c > 0 or \displaystyle ax2+bx+c \geq 0 ax2 +bx+c 0 or \displaystyle ax2+bx+c < 0 ax2 +bx+c < 0 or \displaystyle ax2+bx+c \leq 0. Step 3) Substitute a test number from each interval into the original inequality. General form of a quadratic inequality, after moving all the expressions to one side of the inequality, is in one of the forms which are shown below. This interval is labeled with the letter "C". Lastly, we have an interval that consists of any number that is greater than 6. Plot these critical values and assign signs using the wavy curve method. Students will solve quadratic inequalities and match each inequality with its solution set. values at which the expression becomes zero. This interval is labeled with the letter "B". Factorise the quadratic equation by putting ax2 + bx + c 0. One interval contains any number less than -1 and is labeled with the letter "A". From shortcut 1, if there is solution for the given quadratic inequality, then follow shortcut 2 to know the. Then we can know whether there is solution or not by using the hints given on the above tables. Inequalities can use the greater than, less than, greater than or equal to, and less than or equal to signs. If (a x 2 + bx + c) and x 2 have different signs,we have to find the value of (b 2 - 4ac). Quadratic inequalities have the form ax+bx+c<0. On the horizontal number line, we can set up three intervals: We have split the number line up into three intervals. If both (a x 2 + bx + c) and x 2 have same signs, then there is solution for the given inequality. These endpoints will allow us to set up intervals on the number line. $$x^2 - 5x - 6 > 0$$ Step 1) We will change this inequality into an equality and solve for x. Quadratic inequalities are almost exactly the same as quadratic equations the main difference is that quadratic inequalities have an inequality sign and.

The endpoints are included for a non-strict inequality and excluded for a strict inequalityĮxample 1: Solve each inequality.

If a test number makes the inequality false, the region that includes that test number is not in the solution set.

If the test number makes the inequality true, the region that includes that test number is in the solution set.

Example 1: Solve for x in the equation: x² 5 x + 6 0. Before we get to quadratic inequalities, lets just start graphing some functions and interpret them and then well slowly move to the inequalities. Lastly, find which of the roots satisfy the inequality. Welcome to the presentation on quadratic inequalities. Secondly, find the roots using an appropriate formula for solving a quadratic equation. Reorganize the inequality so that most of the expression’s parts, expressed as f ( x ), are on one side, with just an inequality connecting them to zero. Solving a Quadratic Inequality: A Step-by-Step Guide Algebraically.

Substitute a test number from each interval into the original inequality First, change the inequality sign to an equal sign. The steps outlined below can be used to solve quadratic inequalities.

While working with quadratic inequalities is, in many ways.

$quadratic inequalities$

Use the endpoints to set up intervals on the number line Like linear inequalities, quadratic inequalities may contain one variable or two variables.

These endpoints separate the solution regions from the non-solution regions.

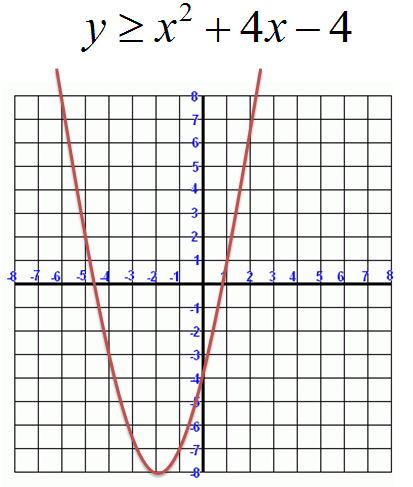
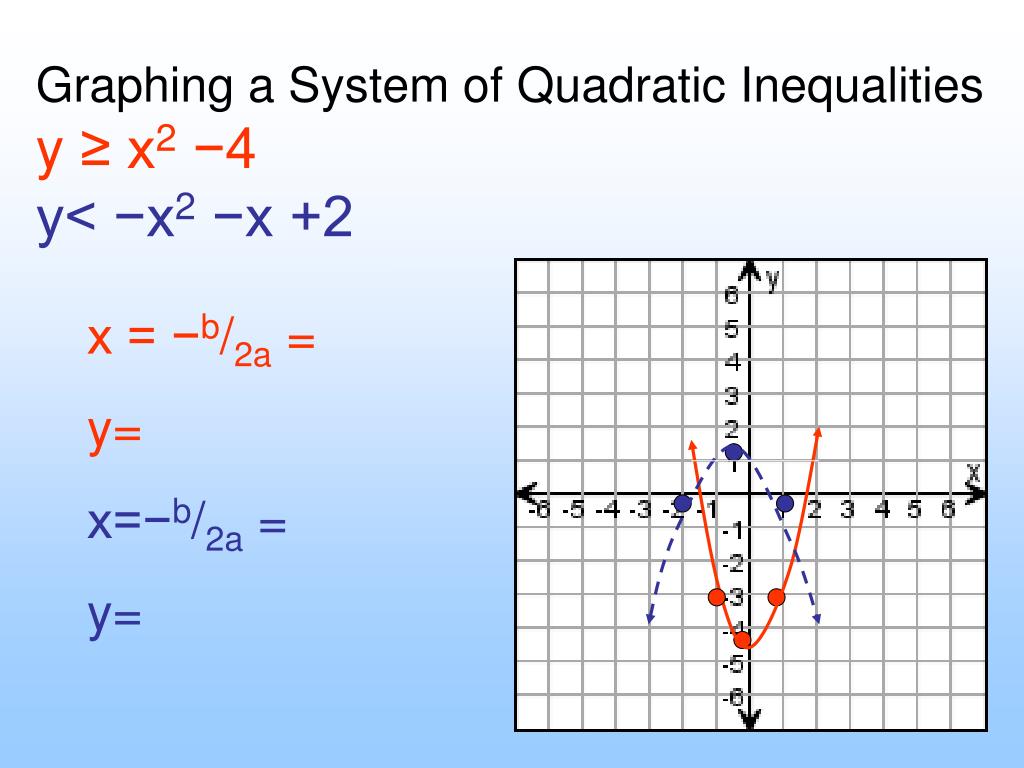
The solutions will give us the boundary points or endpoints.Replace the inequality symbol with an equality symbol and solve the equation.Quadratic Inequalities A quadratic inequality is of the form: $$ax^2 + bx + c > 0$$ Where a ≠ 0, and our ">" can be replaced with any inequality symbol.

QUADRATIC INEQUALITIES HOW TO

$ax^2+bx+c > 0$ or $ax^2+bx+c \geq 0$ or $ax^2+bx+c 0$.In this lesson, we will learn how to solve quadratic and rational inequalities. General form of a quadratic inequality, after moving all the expressions to one side of the inequality, is in one of the forms which are shown below.